مثلث Theorems حاسبة |
| A = | |
| B = | |
| C = | 0 |
آلة حاسبة Triangle Theorems للعثور على خصائص مثلث معين خصائص أخرى مثلث.
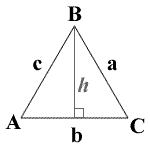
a = الجانب a، b = الجانب b، c = الجانب c
A = زاوية A، B = زاوية B، C = زاوية C، K = المنطقة، P = محيط
في بعض الأحيان، يمكنك أن ترى AAA ASA SAS AAS SSS، فإنها معاني:
AAA = زاوية، زاوية، زاوية
ASA = زاوية، جانب، زاوية
SAS = الجانب، زاوية، الجانب
AAS = زاوية، زاوية، جانبي
SSS = الجانب، الجانب، الجانب
بالنسبة إلى EXMAPLE، إلى SAS: نظرا للجانبين والزاوية بين تلك الأطراف تجد الجانبين والزوايا المتبقية .C = 3، B = 60 درجة، A = 6:
لحساب، استخدم الصيغة التالية: Arccos (B 2 + C 2 - 2 ) / 2BC. عندما تحل محل A، B، و C لقيمها، تحصل على Arccos ((60 2 + 6 2 - 3 2 ) / ( 2 * 60 * 6))، والتي تساوي 90.00005 درجة.
منذ زوايا مثلث يجب أن تضيف ما يصل إلى 180 درجة متساوية 180 درجة، يجب أن يكون C مجموع الزوايا الثلاث تساوي 180.
180 - 3 = 89.99995
89.99995 - 60 = 29.99995
قياس الزاوية الثالثة هو 29.99995 درجة.
حساب ك:
لحساب K، يجب عليك أولا العثور على S. للعثور على S، استخدم الصيغة التالية: S = (A + B + C) / 2.
(A + B + C) = 14.19616 و 14.19616 / 2 = 7.09808، لذلك S = 7.09808.
الآن بعد أن وجدت ق، قد تبدأ بحساب المنطقة. الصيغة لحساب مساحة مثلث
K = (S * (S-A) (S-B) (S-C)).
أولا، قم بتوصيل قيم طول الجانب الخاص بك في الصيغة: K = (7.09808 * (7.09808-6) (7.09808-5.19615) (7.09808-3).
التالي احسب كل حساب جميع القيم الموجودة في الأقواس:
K = (7.09808 * 1.09808 * 1.90193 * 409808).
بعد ذلك، العديد من الأرقام معا: (60.7505).
أخيرا، ابحث عن الجذر التربيعي للنتيجة لإجابتك: K = 7.79426 م 2 .
حساب P:
لحساب P، إضافة جميع الجانبين معا: 6 + 5.19615 + 3 = 14.19615 m.p = 14.19615 م.
مثلث Theorems حاسبة
اختيار اللغة:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.