FoxCalculators - حاسبات مجانية على الإنترنت!

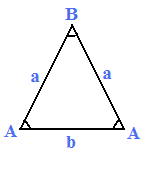
في الهندسة، مثلث متساوي لايفيلس هو مثلث يحتوي على جانبي متساوي طول.

من خلال نظرية مثلث Isosceles، فإن الزوايا المقابلة للجهات المساواة هي نفسها متساوين، في حين أن الجانب الثالث مختلف، فإن الزاوية الثالثة مختلفة.

يمكن أن يحصل حاسبة Isosceles على منطقة ومحيط دائم دائرة نصف قطرها ودائرة دائرة مدرجة وما إلى ذلك.

Isosceles مثلث المعادلات

<فئة الجدول = "القابل للبلد">

<عرض TD = "290"> محيط

<عرض TD = "300"> 2 × A + B

المنطقة (K)

<عرض TD = "300"> k ^{2 = b 2 * (4 × a 2 - b 2 ) / 16}

زاوية بيزيه من الجانب B (T _{B )}

<عرض td = "300"> t _{b ^{2 = 4 × a 2 - b 2 / 2 < / TD>}}

وسائط من الجانب A (M ₎

<عرض TD = "300"> m _{^{2 = (2 * b 2 + 2 ) / 4}}

بزاوية بيزيه من الجانب a (t _{b )}

t _{a ^{2 = b 2 × a × (2A + b) / (a ​​+ b) < سوب> 2}}

<عرض TD = "290"> وسائط من الجانب B (M _{B )}

m _{b ^{2 = (4 * a 2 - b 2 ) / 4}}

دائرة نصف قطرها المدرج (R)

R ^{2 = B 2 × (2A - B) / (4 × (2A + B))}

<عرض TD = "290"> دائرة نصف قطرها الدائرة

<عرض TD = "300"> A / (2 * SIN (A)) أو B / (2 * SIN (B))